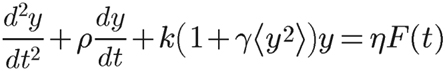You are reading the older HTML site

Positive Feedback ISSUE 65
january/february 2013

The (Un)Broken Audiophile
by David McClain, Acudora, Inc.

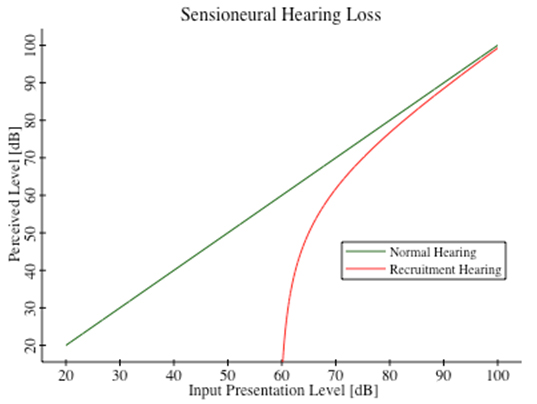
David McClain, PhD Co-Founder, President & Chief Technology Officer of Acudora

Long interested in music and sound, David McClain's varied 40+ year career includes work in astronomy, computer architecture, system software design, and signal processing. His current work is an extension of Dr. Arthur Benade's work in the physics of musical sound. Dr. McClain studied physics and astronomy at Rose-Hulman Institute of Technology but left his undergraduate program early to pursue graduate studies in theoretical astrophysics at The City College of New York. He then completed his doctoral studies in observational infrared astrophysics at the University of Wyoming.

Acudora

Like many companies, Acudora traces its origin to a brilliant and tireless visionary who was inspired by personal circumstances to devise a compelling solution to a complicated universal problem. After his hearing was impaired following a health issue, Acudora, Inc Founder & Chief Scientist David McClain, could no longer fully enjoy his life-long passion for composing and listening to music. Armed with tenacity, a PhD in physics and nearly 30 years of working experience in computer hardware and software design, astrophysics and signal processing, McClain designed experiments to learn the components and limitations of human hearing. After more than a decade of experimentation, calculation and development, David emerged with a comprehensive knowledge of sound and an understanding of how we hear. Using these principles, he created the core technology behind Acudora.

Approximately one in three of us will wind up with damaged hearing due to a combination of illness, exposure to loud industrial noise, or by listening to music played too loudly. The symptoms are typically a loss of high frequency sensitivity. Of those who love sound, it can be a devastating condition and many have simply had to find alternative interests to make up for the loss. Hearing aids are for speech perception but offer nasty surprises for lovers of music, further discouraging any attempt to reclaim the pleasures of being an audiophile.

There is an alternative now, and I want to share with you how we can recover much, and possibly most, of what may have been lost. It begins with a solid understanding of hearing.

Introduction

As you may know, hearing damage is cumulative over the course of a lifetime. It can be accelerated by exposure to damaging levels of sound—factory noise, unmuffled motorcycle riding, or listening through headphones or at live concerts to music played too loudly. What, exactly, happens in the course of hearing damage is still an area of active research. It may be biochemical inhibitors, or structural damage. Schematically, we speak of the death of hair cells. Lizards can regrow damaged hair cells, but so far, humans cannot.

Our hearing begins in the cochlea, but the cochlea is not our hearing. Combined with frequency selective loudness receptors in the cochlea, we also have the afferent 8th nerve, brain and brainstem processing, and efferent 8th nerve. It is a complex feedback control and sensing system. Our hearing is the whole of this system.

Zillions of dollars have been spent over many decades on cochlear research. It is still ongoing, and some of their models are intriguing. But overall, after all the complexity they have found, we seem no closer with that approach toward understanding the whole of human hearing at normal everyday loudness levels.

I'm an Astrophysicist by training. I tried to measure the length and breadth of our Universe; the birth, age, and evolution of stars. I had to work from a distance, since nobody has ever been able to touch a star, let alone travel to the next one in our own neighborhood. I learned that you first try to solve a problem on the back of an envelope before embarking on deeper quests. If you can't reason things out simply at first, then you don't understand enough about the problem to waste time and money pursuing it any deeper. I'm also a signal and image processing expert, and a computer language expert. In short, I'm a "Rocket Scientist''.

I came down with an illness in 2000 that left my own hearing severely damaged. My wife urged me to try hearing aids and I did. I hate hearing aids, and so does everyone else who has ever used them. But they are better than nothing. However, they are intended to restore speech perception, not music. With that goal in mind, they can creatively distort sound to assist in the recognition of speech.

It is easy to distort sound to improve speech perception—people have been doing it for nearly 100 years now. The conventional land-line telephone only transmits a limited portion of the vocal spectrum, from around 250Hz to 3kHz. And that is sufficient to convey the spoken word. In fact, if you included more bass frequencies it would tend to muddle the results.

But hearing aids do really nasty things to music. Noise cancellation, improper compression curves, overcorrected frequencies—oboes begin to sound like muted Jazz trumpets. [What is Miles Davis doing in the middle of this piece from Mozart?] I cannot tolerate listening to music through hearing aids. And I wear some of the best that technology has to offer.

So with my background I was determined to find an answer to restoring musical hearing. It took nearly 12 years to arrive at a pretty good solution. But I have arrived.

My hearing can best be described as a pair of woofers, with a roll-off of 24dB/octave between 1kHz and 1.5kHz. Threshold level sensations need about 60-70dB of assist above 2kHz. But that doesn't mean I need to amplify all high frequencies by 60dB in order to hear them. And if you have hearing damage, you shouldn't try that at home either.

Part of my desire to explain how to restore musical hearing is to also help prevent dangerous practices by desperate people. Simple equalization, as with a standard Graphic EQ, is a dangerous way to help recover your hearing. To understand why, let's examine what happens in damaged hearing, typical of sensioneural hearing loss.

Recruitment Hearing and Dangerous EQ

In the 1950's Dr. Bekesey was awarded the Nobel Prize for his Position Theory of Pitch Sensation. He was working on cat cadavers and noticed that if you unrolled the cochlea, there were particular locations along the basilar membrane that responded most strongly to various pitched tones. The highest frequencies were dealt with by regions closest to the oval window, where sound enters the cochlea. Bass frequencies were handled by the apical region of the cochlea.

Human hearing can be described as consisting of about 24 Bark frequency bands, named after the composer Barkhausen. These are not hard-wired frequency channels, but rather, self-organizing bands, each of which is known as a critical bandwidth of hearing. Two tones within one Bark bandwidth of each other will tend to act a one, in some sense, forming a Bark channel around themselves. It turns out that Bark frequency also corresponds pretty closely to linear distance along the basilar membrane in the cochlea. In terms of conventional frequency units, a Bark bandwidth is nearly logarithmic above 500Hz, but nearly constant bandwidth of around 100Hz below that frequency.

When a particular frequency region is damaged in sensioneural loss, it responds to loudness in a manner known as recruitment hearing. At near-threshold levels you need a significant amount of boost to hear the test tones. But as the tones grow louder, you have less and less trouble hearing them until, at the very loudest levels, your hearing becomes pretty much normal, just like everyone else's.

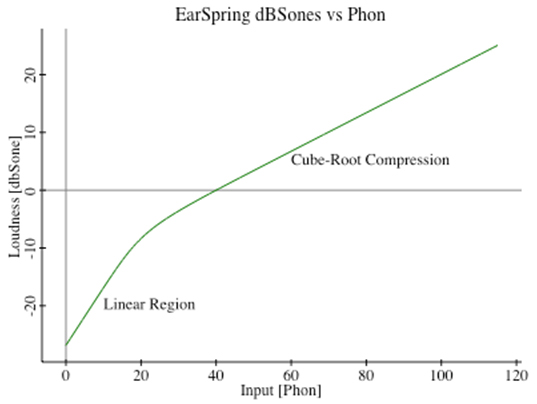
Recruitment hearing for a threshold elevation of 60 dB.

In Figure 1 we have a schematic illustration of recruitment hearing versus normal hearing. The green line for normal hearing shows that what you perceive is what is being presented. The red curve for recruitment hearing shows that as sound levels decline, they decline very rapidly—as for gain expansion, until below the elevated threshold level, they disappear entirely. But at loud presentation levels you can see that recruitment hearing asymptotically approaches normal hearing. You need tons of help to hear threshold levels, and almost none to hear very loud levels.

So you can see that if you just provided a constant gain of 60dB to sounds in this damaged frequency region, you would quickly gain too much as your hearing tends toward normalcy at very loud levels. The first time I did this, out of my own ignorance, I was listening to the 3rd movement of Scheherazade, and when the trumpets blared it knocked me off my seat. This is a dangerous thing to do.

What you need to do instead is provide dynamic equalization, or nonlinear compression, to that frequency band, so that as the sound grows louder, you get less and less gain applied to the signal. You need to provide a compression curve that is complementary to the gain expansion produced by recruitment hearing.

So great... that's the principle involved... how do you know how much compression to apply at any sound level?

The EarSpring Equation

Starting as I did with already damaged hearing, I needed a reference for normal hearing. What should things sound like? As you know, our acoustic memory is very faulty. I had no idea how things ought to be sounding.

As a youngster, I met Dr. Arthur Benade in his laboratory in the basement of Case-Western Reserve University, just behind the walls housing their Van de Graf Generator in the Physics building. I was a clarinetist, and so was he. He had an optical bench set up with all kinds of equipment to measure and understand the effects of exit flaring on horns and clarinets. Fascinating... Dr. Benade is also the author of a famous text, the “Fundamentals of Musical Acoustics”. In that book he recounts what has been known for quite some time, and adds a lot of his own discoveries.

So what have we known for a long time? One thing we know is that human hearing is compressive by nature. It takes a 10dB increase in sound pressure level to sound about twice as loud. This is the only way we can accommodate a 120dB dynamic range in our hearing without ripping our cochlear structures to shreds. Our hearing is roughly cube-root compressive at normal everyday sound levels.

We also know that near threshold levels, our hearing becomes very linear in a physics sense. You put in a sine wave of very small amplitude and you get a directly proportional sense of loudness.

The linear nature of threshold hearing, and the cube-root compressive behavior at normal sound levels, has been known for at least 50 years.

What else do we know? I played the violin in college. My teacher taught me to play flat because as tones grow louder to our ears they grow progressively flatter. But for persons listening in the audience, where the violin is not right next to their ears, they don't hear the pitch flattening. And if the violinist tried to correct his playing to his own sense of correct pitch, he'd end up sounding sharp to the audience.

In fact, my lab measurements have shown that around 1 kHz, the pitch flattening is as much as 75 cents, or 3/4 of a semitone, as the sound grows from 40dB SPL to 90dB SPL. Try that out at home, and you'll quickly sense the pitch flattening for yourself.

So, while the accumulation of knowledge took some time in my lab, and I wrestled for the simplest possible equations that could explain these phenomena, I finally did arrive at the equation I call EarSpring that represents normal human hearing.

The EarSpring equation representing normal hearing.

EarSpring is a relatively simple equation, compared to current cochlear models. It is an analog of the whole of our hearing—not just a cochlear model. It behaves grossly in the same manner as normal hearing, and serves as a reference at any particular frequency for what things ought to sound like.

It is, ignoring the γ term in brackets, an equation for a damped harmonic oscillator—a spring. The γ term says that the stiffness of the spring increases with the average power of vibration of the spring. It gets stiffer as sound excitation grows louder and causes the spring to vibrate more vigorously. This growing stiffness provides some resistance against unconstrained vibration amplitudes—cube root compression. And it causes the resonant frequency to shift upward, which matches the flattening of pitched tones as they grow louder. [...this is not a contradiction, but it might take you a few minutes to reason it out...]

EarSpring is a nonlinear differential equation, and describes whole families of solutions. By applying what we know about hearing to this equation, the so-called boundary conditions, we select out a particular solution.

The particular solution for EarSpring that satisfies the boundary conditions.

Consequences of EarSpring that serve to verify its correctness include, among other things, the gradual generation of odd harmonics in the bass region as sounds grow louder. EarSpring predicts this effect in simulations, and lab measurements verify this in practice.

Another easy prediction is nonlinear mixing in our ears, where two tones of nearby pitch produce a beating effect. This cannot (shouldn't!!) happen in an Earthworks microphone. It requires nonlinearity in the sensor.

And then there are the 3rd order IMD (InterModulation Distortion) products arising from two tones, and can easily be measured using the probe tone techniques developed by Julius Goldstein while at MIT and the Harvard Psychoacoustics Laboratory.

My lab measurements show that at loud, but comfortable, levels of music, we ought to be swimming in IMD products. And one possible indictment against lossy compression methods is that the elision of certain frequency components deemed hidden by loudness masking, will also remove the possibility to generate expected IMD products in unmasked regions.

We don't normally notice these IMD products because we grew up immersed in them. But if you ever develop a deep notch in your hearing, you just might notice their effects by omission. I certainly do...

I have a profoundly deep notch (>90dB) in my left ear at around 1250 Hz. When I listen unassisted to high string sections, or female choral music, I hear what sounds like I'm walking on gravel. If I reduce 2kHz by as little as 2dB the effect disappears almost entirely. Conversely, if I boost 2kHz by as little as 2dB, the effect becomes significantly stronger.

This extreme sensitivity of the effect to small changes in amplitude at 2kHz is suggestive of high-order IMD. Why gravel? My brain was trained on a full presentation of sound fields as a child. Now that I have some missing presentation, the brain associates as best it can?

The Conductor Equation

Now that we know how things ought to sound, another equation provides the loudness response of how things do sound to recruitment hearing. I call this equation the Conductor equation. This, coupled with EarSpring provides the shape of the recruitment curves, relative to normal hearing.

I'll spare you the detailed equations, but note that different degrees of impairment imply different levels of threshold elevation. And there is one recruitment curve for every particular threshold elevation. With sensioneural hearing loss, the threshold elevation varies by frequency, generally increasing toward higher frequencies.

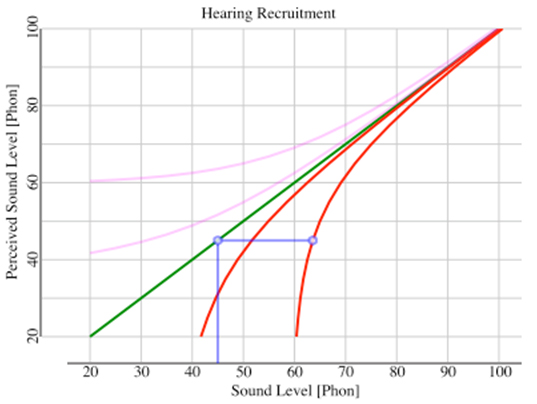
Figure 4 - Showing how to correct for recruitment hearing. Presentation level is 45 Phon, threshold elevation is 60dB, needed gain is light-blue horizontal segment. Light pink curves in the upper region of the graph illustrate the complementary compression curves needed to cancel the gain expansion curves from recruitment hearing.

So if I now know, at each frequency, how things ought to sound, and then how they do sound under recruitment hearing, then I also know how to make the nonlinear compressive correction. The particular recruitment curve to use is dictated by the measured threshold elevation at each frequency. See the description accompanying Figure 4.

The Crescendo Solution

Now, imagine a signal processing system that divides the audible spectrum into Bark frequency bands, spaced at quarter-Bark spacing because these are self-organizing bands, not hardwired channels. And in each of these 100 bands, it computes how things ought to sound at any moment, and how they do sound to a particular level of hearing impairment. And knowing the difference between these two loudness levels, it applies a corrective gain. And it does this more than 300 times per second, and in full stereo.

That system exists, and I call it Crescendo. I have been using variants of it for more than 10 years. It served as my prototype and vehicle for learning and experimentation. I have shared it with others so that they may enjoy what it brings, each Crescendo system tuned to their specific hearing needs.

Crescendo applies frequency selective nonlinear compression. Or another way to look at it is to call it dynamic equalization. Its temporal response in each frequency band needs to match the temporal masking profile of our hearing, so that it doesn't pump.

There is no noise cancellation, as that would erode bass and drone sounds which are important to music. It does not creatively distort harmonic content to assist in speech perception. Rather it specifically honors the harmonic spectra of musical instruments to keep oboes sounding like oboes, not like muted Jazz trumpets.

Complexities arise because this system has to run on a real processor. A decade ago there weren't many processing CPU's that could handle the load. But over time we gained new advances in CPU design, and we discovered clever approximations to the system of nonlinear differential equations, and so now it can now be handled quite easily with today's multicore processors.

Secondly, we need to avoid the generation of spurious harmonics of the processing rate. Early designs exhibited plenty of nasty harmonics and sub-harmonics under certain pure-tone conditions. Today, we have smooth processing that avoids things like temporal aliasing and spurious harmonic generation, so that our strongest spurs are more than 120dB down from the carrier level.

Thirdly, the EarSpring equation says that corrections need to be based on average power levels. But impulsive sounds, like drum strikes, are so short that, despite their strength, they barely register to a running RMS calculation. Hence we needed to augment this with crest-factor analysis, to prevent excessive gain being applied at the height of drum strikes.

Initially, I used audiology measurements to set up the corrections in each Crescendo unit. But that proved to be a problem because (A) audiology is very inaccurate, all the more so at frequencies with significant damage, and (B) there are effects detected at threshold levels that do not apply at normal everyday loudness levels. We simply don't live in a threshold level world.

Worst among the threshold effects is a precipitous drop in threshold elevation between the onset frequency of impaired hearing and the lower frequencies with normal hearing. This causes audiologists who tune hearing aids in accordance with their patient's audiograms to overcorrect the region, typically between 1-2 kHz. Mixing engineers call this frequency region the pain frequencies, and most hearing aid wearers complain about their sound, principally because of this unrecognized overcorrection. [1-2kHz is the approximate sound of a cheering crowd in a football stadium]

One-Knob Adjustment

So back to the drawing board, er, rather, the back of another envelope... Let's think about hearing damage as occurring from the introduction of damaging levels of sound to the hearing system. There will be variations from person to person in their susceptibility to hearing damage.

But hydrodynamics dictates the sonic excitation in the fluid filled cochlea. As such, the rate of decline of damage as one proceeds deeper into the cochlear chamber ought to be more or less the same between individuals. What differs is the amount of damage.

And when power dissipates along some direction, the amount of power given up is proportional to the amount of power remaining at any point. In other words we should see an exponential decline in the damage level. In terms of dB measure, this becomes a straight line with distance along the basilar membrane, or equivalently, with decreasing Bark frequency.

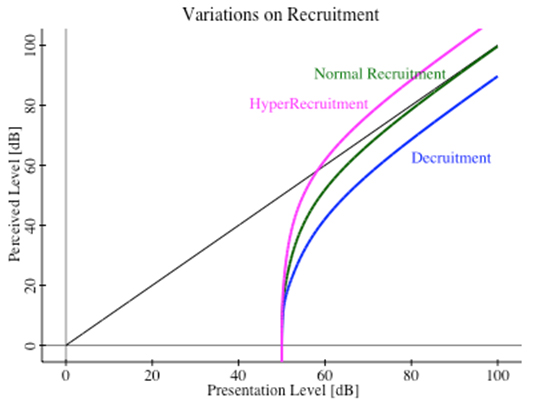
The Crescendo control panel, showing the 1-knob tuning, called vTuning (for lack of a better name) in this image.

So, voila! We can tune for gross sensioneural hearing loss with a single knob adjustment. We have a pretty good idea what the constant dB/Bark slope should be, and so the knob simply adjusts for the overall amount of damage at any particular location.

This is a huge simplification to the tuning of hearing corrective systems. And it allows each individual to tune the system for themselves. Once tuned up, you just leave it running and never touch it again. Just pipe all your sound through it on the way to headphones or speakers and sit back and enjoy your sound just like you always used to do.

Variations of Recruitment Hearing

To be sure, individuals will exhibit variations from a straight-line dB/Bark solution. Exposure to ototoxic medications (e.g., Aspirin, chemotherapy), radiation, illness, and other causes, may produce dips and peaks along the slope. But underlying all these variations should be a gross linear decline in hearing damage levels—at least for nearly typical sensioneural hearing loss.

There is a condition called hyper-recruitment that produces sounds growing too loud too quickly as their presentation level increases - often to the point of discomfort. Another variation called decruitment has that sounds never quite sound as loud as they ought to, even at very loud presentation levels.

In actual fact, all four conditions—normal hearing, normal recruitment, hyper-recruitment, and decruitment, may coexist in different frequency regions for some listeners.

Variations of recruitment hearing - normal, hyper-, and de-cruitment.

A fortunate byproduct of our clever approximations shows that the level of corrective gain needed depends principally on the difference between the threshold elevation and the presentation loudness. In such case, we can commute the operations of gain/attenuation with our nonlinear corrections. And we can handle situations of hyper-recruitment with an EQ dip ahead of Crescendo, and decruitment with an EQ boost ahead of Crescendo. In fact we can also provide second order corrections for your headphones and speakers in this manner.

There are no audiology tests to quantify the degree of hyper-recruitment or decruitment, nor even to detect which frequency regions have these conditions. Audiology exams will often discover a narrowed range of comfortable sound levels, which is a hint that hyper-recruitment may exist.

A careful, detailed, analysis of one's own hearing can reveal the frequency locations for each kind of recruitment. And the pre-EQ adjustments ahead of Crescendo have to be experimentally developed in amplitude.

Ideally these pre-EQ treatments should be applied in Phon space. But using conventional equalizers, which apply their corrections in dBSPL space, is a decent enough approximation to be useful.

As an example, my own hearing exhibits normalcy below 1kHz, then it grows into recruitment hearing. At around 1.6kHz I have a narrow region of hyper-recruitment, and above 4kHz I have decruitment hearing. So when I use Crescendo, I dip 1.6kHz by as little as 2 dB, with a Q = 0.707 to deal with the hyper-recruitment. And for the decruitment portion I use a gentle 4 kHz high-shelf boost of 6dB, also with a Q = 0.707.

It doesn't take much additional pre-EQ, on top of what Crescendo already supplies for the gross damage slope. With a customized version of Crescendo for myself, I do apply these in Phon space. But initial experiments in conventional dB SPL space sounded very similar and quite good.

Psychological Effects

As a result of using my Crescendo correction system, I now have what I claim to be "Golden Ear" hearing. I normally live in a very dark world. Before I embarked on this journey my own musical compositions migrated to the lowest registers of the keyboard, below 250Hz, or middle-C. As a result, like someone attuned to the dark, I notice every little detail of sound when presented with the opportunity.

I hear the buzzing of her fingernails as the harpist plays a Boildeliu Concerto. I hear her knuckles knocking against the wooden harp frame during her playing. You could notice these sounds too, except for the fact that you are inundated with extraneous noises throughout the day, and your mind has learned to ignore most of it. But for me, in this dark world, the use of Crescendo makes each of these artifacts sparkle like gemstones in the sunlight.

Without assistance, I can't even hear my own sibilance. But with Crescendo I get to hear the almost magical S's of my wife's speech up around 10 kHz. Crescendo can't work complete miracles however. The region above 10-12kHz, the so-called air, is lost to me forever. Profound hearing loss can never be restored. But there is a huge, wonderful, acoustic spectrum below that cutoff, and most of music exists down there to be heard.

What's Different Here?

What is the difference between Crescendo and a "hearing aid for your stereo system''? On its face, none. But Crescendo's lineage springs from first principles of physics. And hearing aids arise from a world largely ignorant of physics, and almost wholly dependent on patient surveys among untrained subjects.

I have an advantage as a trained listener, and as a physicist. I can recognize and understand acoustic phenomena, and I have the vocabulary to express their details. Untrained listeners can only respond as best they can—much like our ancient's descriptions of "comets swallowing the Earth''.

As a result, I have exponents of nonlinearity for the human hearing loudness response that are grounded in physics principles. When you examine the design of many hearing aids one finds that they are using wholly incorrect exponents of nonlinearity, leading to gross overcorrection. Others may understand proper values, but are intentionally distorting sounds in the hopes of enhancing speech perception. Universally, hearing aids are tuned on the basis of threshold audiology, despite the fact that they are never used in such conditions.

Almost all high-end digital hearing aids today use WOLA filter banks, akin to FFT analysis. And a byproduct of this is to apply hearing corrections to bands of constant bandwidth. This is a gross mismatch to our hearing, which is better described as self-organizing Bark bands, whose bandwidth increases nearly logarithmically toward higher frequencies. As a result, FFT-like processing is applied to weaker levels of acoustic power, since almost all sound exhibits a spectral roll-off of around 6 dB/octave or more. And hence the relative error in their corrections becomes more apparent.

The use of FFT-like processing, mismatched to the widening bandwidth of Bark channels, gives rise to the marketing lie about how many bands are invoked in the latest digital hearing aids. My own 15-band high-end digital hearing aids are really only covering about 3.5 Bark bands, or about 1/7 of the audible range. Crescendo covers the entire audible range with matched bandwidth processing.

As for tuning, we are unique in allowing people to tune up their own hearing corrective system. Threshold audiology may serve a guide, but ultimately we are correcting sound at normal everyday loudness levels, not at threshold levels. We know the shape of recruitment hearing curves, so no need to allow for adjustable multiple-breakpoint compression curves.

By applying physics to the problem, we have reduced a potentially 150+ variable problem (multiple frequencies, compression slopes, gains, thresholds, multiple breakpoints) to a one-dimensional problem amenable to single-knob adjustment.

And finally, we are unique in being able to directly correct for hyper-recruitment and decruitment variations on normal recruitment. To the best of our knowledge this has never before been accomplished. It took the realization that gain/attenuation could commute with the nonlinear corrections derived from physics for this to happen.

Addendum

I've just made it even easier for everyone to try out Crescendo on their Mac computers. There are 3 files to download:

http://refined-audiometrics.com/tekram/CrescendoLive-Installer.pkg  (12 MB)

http://refined-audiometrics.com/tekram/Acudora-Save-Shares.app.zip (5 MB)

http://refined-audiometrics.com/tekram/eval-license-03012013.txt (1.4 KB)

Install with the installer. Either before or after that, but before attempting to run CrescendoLive.app, be sure to unzip and run the Acudora-Save-Shares.app. Copy the entire contents of the eval license text file and paste into the Acudora-Save-Shares text window and hit the Save License button.

This permits the evaluation copy of CrescendoLive to run on any Intel Mac computer (Mac-Mini, MacBook, tower systems, etc.), until 1 March 2013. There are no limitations in this version, except to state that it will cease functioning after March 1 of this year.

Nobody needs to contact me unless they wish to do so. If people feel they need longer to evaluate the system, they can contact me for a different license.

To reiterate the settings I use on my MacBook, I listen to WAV uncompressed audio files through iTunes, piped through our AcudoraPipe to CrescendoLive for processing, then out to a Lavry DA11 and into either KRK Nearfield Monitors, or my Beyerdynamic DT-880 or Sennheiser HD650 headphones for listening.